Un article très intéressant est paru sur la BBC traitant des problèmes liés au diagnostic de maladies comme le cancer. Les problèmes naissent du fait que les les personnes saines sont plus nombreuses que les personnes malades (prévalence de la maladie basse) et que le test diagnostic peut être positif (i.e. la maladie est détectée) bien que le patient soit sain (taux de faux positifs différent de 0). Cela veut dire que même si le test est positif, les chances sont toujours hautes que la personne soit saine.

Exercice tiré de l’article

Quelle est la probabilité qu’une femme testée positive (i.e. malade) à une mammographie soit malade étant données les données suivantes ?

1. La probabilité qu’une femme ait le cancer du sein est de 1% (prévalence).

2. Si une femme a le cancer du sein, la probabilité que le test soit positif est de 90% (sensibilité du test).

3. Si une femme n’a pas le cancer du sein, la probabilité que le test soit quand même positif est de 9% (taux de fausse alerte).

Réponses possibles

a. 90%

b. 80%

c. 10%

d. 1%

Danse l’étude présentée par l’article, plus de trois quarts des médecins présentés avec cette question ont répondu faux ! Beaucoup (presque la moitié) ont répondu 90%, peut-être en raison du point 2 ci-dessus (probabilité que le test soit positif si la femme a le cancer). Cependant, la question est la probabilité que la femme ait le cancer si le test est positif ! Ce n’est pas la même chose !

Pour répondre à la question, il faudra rouvrir les cours de probabilité, en particulier il faut utiliser le théorème de Bayes.

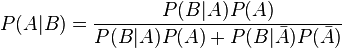
Adaptons le théorème à notre cas particulier.

A : la femme a (vraiment) le cancer

B : le test est positif, le diagnostic suggère que la femme a le cancer

P(A | B) : étant donné que le test est positif (condition), la probabilité que la femme ait vraiment le cancer du sein

Les barres au-dessus des lettres indique la négation.

En remplaçant les probabilités données dans l’exercice dans la formule, nous obtenons ceci:

 

ce qui est environ égal à 10% ! bien loin des 90 % suggérés par les médecins.

Notez que le 99% (probabilité de ne pas avoir le cancer du sein) est le complémentaire du 1% (probabilité d’avoir le cancer du sein, sans a priori).

Cristian Riccio, le 7 juillet 2014

Références

article de la BBC
Théorème de Bayes sur Wikipédia